της Δήμητρας Σπανού Χημικού καθηγήτριας στο 1ο Γυμνάσιο Δάφνης
Όπως έχει αναφερθεί
Ο Λογισμός είναι ένας κλάδος των Μαθηματικών που επιτυγχάνει να έχει διαρκή αποτελέσματα κατά την διάρκεια των μεταβολών αυτών, είτε όσον αφορά τον τρόπο που γίνονται (κλίσεις καμπυλών στον διαφορικό λογισμό) ή τον υπολογισμό των συνολικών ποσοτήτων που παράγονται κατά την διάρκεια των μεταβολών αυτών με τον ολοκληρωτικό λογισμό
Στον Διαφορικό Λογισμό περιλαμβάνονται οι Σύνηθεις και οι Μερικές Διαφορικές Εξισώσεις
Γραμμικές Διαφορικές Εξισώσεις 2ης τάξης
Η γενκή εξίσωση μπορεί να περιλαμβάνει δεύτερη παράγωγο, πρώτη παράγωγο, την συνάρτηση ως προς συγκεκριμένη μεταβλητη και σταθερό όρο. Αν ο σταθερός όρος είναι 0 έχουμε γραμμική δεύτερης τάξης ομογενή
y΄΄ + y΄ + y =g(x)
Διακρίνουμε περιπτώσεις
1. 2ης τάξης τύπου y΄΄ + poy =0
παραδείγματα:
α. Εξίσωση ελατηρίου
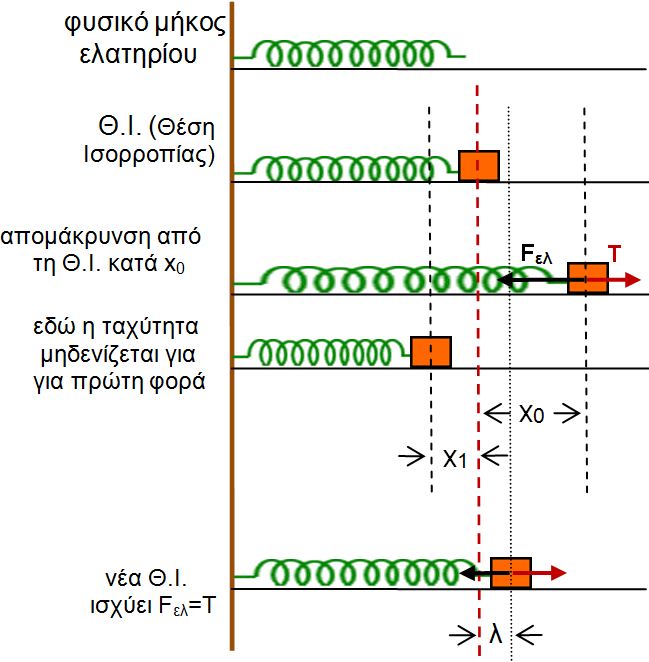 Οι δυνάμεις στον ταλαντωτη είναι η τάση Τ = -kx (Η Δύναμη που ασκείται στο ελατήριο για να επιμηκυνθει κατά x είναι kx)
Οι δυνάμεις στον ταλαντωτη είναι η τάση Τ = -kx (Η Δύναμη που ασκείται στο ελατήριο για να επιμηκυνθει κατά x είναι kx)
Η δύναμη επαναφοράς προσδίδει επιτάχυνση α F επ = mα.
H μετατόπιση είναι x
H ταχύτητα στον ταλαντωτη είναι η πρώτη παράγωγος της μετατόπισης dx/dt =y (ταχύτητα)
Η επιτάχυνση στον αρμονική ταλαντωτή θεωρείται η δεύτερη παράγωγος της μετατόπισης ίση με α= d2x/dt2
Η δύναμης επαναφοράς είναι ky ( k σταθερά του ελατηρίου)ενώ η Γνωρίζουμε πως η επιτάχυνση είναι η δεύτερη παράγωγος του διαστήματος ως προς χρόνο. Άρα F επ = md2x/dt2)
F επ -Τ =0
md2x/dt2 - kx =0
β. Εξίσωση Εκκρεμούς (αρμονικός τακαντωτής)
Α. Εξίσωση Ricatti dy/dx = Q(x)y2 + P(x)y+ G(x)
Eκτός από τον Bernouli o Riccati διατυπώνει μια εξ ίσου γνωστή διαφορική εξίσωση 2ου βαθμού
dy/dx = Q(x)y2 + P(x)y+ G(x)
οι Q(x) , P(x), G(x)
είναι συνεχείς συναρτήσεις ορισμένες σε ένα διάστημα Ι που ανήκει στους παγματικούς αριθμούς.
Αν το Q(x)=0
η εξίσωση Riccati ειναι η Bernoulli.
Αν Q(x)=0 είναι μη ομογενής γραμμική ΔΕ ( dy/dx = P(x)y+ G(x)
d i/ dt + R L/ i = E/ L i= i(t):
Αν G(x)=0 είναι Bernoulli με α=2 dy/dx + P(x)y = Q(x)y2
Την Εξίσωση Ricatti λύνουμε συνήθως με μετασχηματισμό
Στις εφαρμογές της συμπεριλαμβάνεται και η εξίσωση Strondinder στην περίπτωση που είναι ανεξάρτητη από τον χρόνο και σε μια διάσταση
Μη Γραμμικές Διαφορικές Εξισώσεις ανώτερου βαθμού
Κατηγορία ΔΕ που με μετατροπές τους καταλήγουν σε γραμμικές
Δ
Παράδειγμα μεταφορά από σχολικό
Από τη Φυσική γνωρίζουμε ότι στο διπλανό κύκλωμα ισχύει ο κανόνας του Kicrhhoff. Δηλαδή, |
|
 |
|
Αυτή ισοδυναμεί με dI(t)/dt +R/L I(t) = 1/L .V(t)
Εδώ έχουμε I=y και t=x P(x)y=R/L.I(t) και 1/L .V(t) =q(x)y0
|
αν α=1 η εξίσωση γίνεται dy/dx + [(p(x) -q(x)]y =0και είναι μια γραμμική ομογενής
H εξίσωση για να λυθεί, Εκτελούμε μετασχηματισμό :u(x) ={y(x)} 1-α και το πρόβλημα μετατρέπεται σε γραμμικό
du/dx + (1-a)p(x)u = (1-a)q(x)yα
u(xo) =yo1-a
Επιλύθηκε από τον Γερμανό Leibniz με την χρησιμοποίηση της αντίστροφης συνάρτησης y(x) = (u(x) )1/1-a
Πρέπει ο εκθέτης να είναι ακέραιος. Αν είναι περιττός θέτουμε την w(x) = - y(x) και μετά μετασχηματίζουμε

σταθερό Ο πρώτος όρος ρ
ε παριστάνει την ενέργεια από τις εξωτερικές δυνάμεις ο δεύτερος την δυναμική πίεση που είναι μέρος κινητικής ενέργειας του ρευστού και ο τρίτος την υδροστατική πίεση που είναι μέρος της δυναμικής ενέργειας λόγω στατικού υψους.
Διατυπώνει το 1695 την ομόνυμη διαφορική εξίσωση Bernoulli
dy/dx +p(y)x =q(x)yα
,
Όπου θεωρούμε υγρό μέσα σε σωλήνα που μετατοπίζεται από το σημείο Α στο Β. Η για στοιχειακή μετατόπιση στον άξονα των χ ισχύει η πάνω εξίσωση .
Αν ο εκθέτης α =0 τότε είναι γραμμική αν α=1 τότε είναι γραμμική ομογενής (χωριζόμενων μεταβλητών)
Αν ο α είναι διαφορετικός από 1,0 τότε έχουμε μη γραμμική εξίσωση . Οι p(x) και q(x) είναι συνεχείς συναρτήσεις σε ένα διάστημα
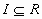 ,
, 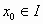 , και
, και 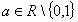 .
.
Γ, Διαφορικές εξισώσεις Leonhard Euler
Μηχανική :
Για την περιγραφή σύνθετων και περίπλοκων προβλημάτων Μηχανικής

Οι διαφορικές εξισώσεις περιγράφουν πιο περίπλοκα προβλήματα κινηματικής και Δυναμικής όπως:
-Κινήσεις που υπόκεινται σε δεσμούς. παράδειγμα ένα σώμα που κινείται πάνω σε σφαίρα
- Περιγραφή συστημάτων που αποτελούνται από Ν σώματα και πρέπει να χρησιμοποιηθούν 3Ν συντεταγμένες (3 καρτεσιανές για το κάθε ένα), στα οποία πολλές φορές απλούστευονται με άλλες μεταβλητές όπως με την χρησιμοποίηση πολικών ή σφαιρικών συντεταγμένων
-Γενικότερα Συστήματα με μεταβλητές οι οποίες είναι ίσως κατάληλες για το συγκεκριμένο κάθε φορά σύστημα (Γενικευμένες Συντεταγμένες), τις οποίες πιθανόν να πρέπει να μετασχηματίσουμε σε καρτεσιανες συντεταγμένες . Παράδειγμα να πρέπει να μετατραπούν οι πολικές σε καρτεσιανές συντεταγμένες οπότε μετασχηματίζουμε οι πολικές συντεταγμένες
r,θ, οπότε έχουμε
x1=rcosθ,x2=rsinθ.
Όσα υλικά συστήματα μπορούν να εκφραστούν με διανυσματικές συναρτήσεις (ολόνομα) και άλλα μη ολόνομα (εκφράζονται με ανισότητες ή μη ολοκληρώσιμες σχέσεις)
Από τα ολόνομα σε άλλα οι δεσμοί τους είναι ανεξάρτητοι του χρόνου και σε άλλα όχι (σκληρόνομα- ρεόνομα).
Παράδειγμα αν μελετάμε την κίνηση ενός υλικού σώματος πάνω στην επιφάνεια μιας σφαίρας (ολόνομο σύστημα). Αν η ακτίνα της σφαίρας είναι σταθερή έχουμε ένα σκληρόνομο σύστημα ενώ εάν μεταβάλεται με τον χρόμο ένα ρεόνομο.
Στο παράδειγμα αυτό για να περιγράψουμε την κίνηση πάνω στην επιφάνεια μιας σφαίρας πρέπει να μελετήσουμε όλες τις δυνατές θέσεις πάνω στην επιφάνεια της σφαίρας
Ένα αντίστοιχο παράδειγμα κίνησης με δεσμό είναι η κίνηση ενός σώματος που κρατά ένα σημείο του σταθερό οπότε οι δυνατοί μετασχηματισμοί είναι το σύνολο των περιστροφών του.
Αυτού του είδους οι κινήσεις που είναι πολύ δύσκολο να μελετηθούν με τους αρχικούς τύπους των εξισώσεων της μηχανικής .
Το θέμα είναι εκτεταμένο και έτσι έγινε προσπάθεια οι διαφορικές εξισώσεις που επιλύουν τέτοιου τύπου προβλήματα να εξάγονται από μια γενική αρχή
Σε ότι ήταν ήδη γνωστό και περιγραφόταν από τις εξισώσεις του Νεύτωνα, έπρεπε να δωθεί με μια διαφορετική διατύπωση , ακόμα και με την χρησιμοποίηση γενικευμένων συντεταγμένων,
Αυτό γίνεται με την βοήθεια μιας συνάρτησης L που ονομάζεται συνάρτηση Lagrange
Σε αυτές το υλικό σύστημα μπορεί να παρασταθεί με ένα σημείο: q= (q1, q2, q3, ...qm) όπου m ο αριθμός των διαστάσεων (θεσεογραφικός χώρος)
Από την συνάρτηση Lagrange προκύπτουν μια σειρά από γενικευμένες εξισώσεις για δύσκολους υπολογισμούς μηχανικής, οι εξισώσεις Lagrange, όπως για την γενικευμένη ροπή αδράνειας, την ολική κινητική ενέργεια του συστήματος, k.a.
Oι εξισώσεις Lagrange όμως αναφέρονται σε ακίνητο σύστημα αναγοράς και αν χρειάζονται υπολογισμοί για κινούμενο πρέπει να γίνουν μετατροπές
Έτσι για παράδειγμα οι νόμοι της κίνησης θα προκύψουν από την αρχή του Hamilton που βασίζεται στο ολοκλήρωμα της συνάρτησης L στον χρόνο από t1 σε t2
Διατυπώνεται η αρχή ελαχίστης δράσης που έχει μεγάλη σημασία γιατί εκτός των άλλων αποτελεί ένα ισχυρότατο μαθηματικό εργαλείο στην μελέτη των δυναμικών συστημάτων
μεταφέρω από https://users.uoa.gr/~pjioannou/mech2/READING/Hatz_mech2_New.pdf σελ 11
...μέσω αυτής ο δυναμικός νόμος εκφράζεται σε γεωμετρικά αναλύωτη, συμπαγή και κομψή μορφή και οι βασικές αρχές και συμμετρίες που τον διέπουν καθίστανται πλέον ανάγλυφες...
Δ. Εξισώσεις Lagrange y= xg (dy/dx) + f(dy/dx)
 Συνηθίζονται για κινήσεις που υπόκεινται σε δεσμούς ή περιγραφή συστημάτων που αποτελούνται από Ν σώματα και μελετήθηκαν από Γάλλο μαθηματικό Joseph-Louis Lagrange (1736-1813).
Συνηθίζονται για κινήσεις που υπόκεινται σε δεσμούς ή περιγραφή συστημάτων που αποτελούνται από Ν σώματα και μελετήθηκαν από Γάλλο μαθηματικό Joseph-Louis Lagrange (1736-1813).
Η διαφορική εξίσωση y= xg (dy/dx) + f(dy/dx) ονομάζεται εξίσωση Lagrange όπου g(p) και f(p) ορισμένες σε 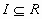
με συνεχείς παραγώγους στο Ι. ,
Θέτοντας p= dy/dx έχουμε y= xg(p) +f(p) και παραγωγίζοντας ως προς χ παίρνουμε
y΄= p =g(p) + xg΄(p)dp/dx + f΄(p) dp/dx και λύνουμε ως προς χ και
η γενική λύση της εξίσωσης Lagrange που προκύπτει είναι x=x(p,c) y=xg(p) +f(p) , pER όπου c είναι μια αυθαίρετη πραγματική σταθερά
και οι ιδιάζουσες λύσεις pi είναι pi* -g(pi*) =0
ΔΕ μεγαλύτερης τάξης για ηλεκτρικό κύκλωμα RLC
RCdVc/dt + LC d2(Vc)/dt2 +Vc =0

ΠΗΓΕΣ
https://tutorial.math.lamar.edu/Classes/DE/Linear.aspx
https://mathbooksgr.files.wordpress.com/2011/12/diaforikes_sourlas_2007.pdf
https://myria.math.aegean.gr/epeaekI/courses/odigoi_askisewn/ODE/odek02/Separable/k02_separable.htm
https://myria.math.aegean.gr/epeaekI/courses/odigoi_askisewn/ODE/odek02/Bernoulli/k02_bernoulli.htm
https://eclass.uniwa.gr/modules/document/file.php/TIO119/%CE%A0%CE%91%CE%A1%CE%91%CE%94%CE%9F%CE%A3%CE%95%CE%99%CE%A3%20%CE%9C%CE%91%CE%98%CE%97%CE%9C%CE%91%CE%A4%CE%A9%CE%9D/%CE%9C%CE%91%CE%98%CE%97%CE%9C%CE%91%CE%A4%CE%91%20%CE%91%CE%9D%CE%A9%CE%A4%CE%95%CE%A1%CE%A9%CE%9D%20%CE%9C%CE%91%CE%98%CE%97%CE%9C%CE%91%CE%A4%CE%99%CE%9A%CE%A9%CE%9D%20%CE%99%CE%99.pdf
Φθίνουσα ταλάντωση με δύναμη απόσβεσης την τριβή ολίσθησης | physicsgg
ακατεργαστο
Οι εφαρμογές των διαφορικών εξισώσεων στα προβλήματα κινηματικής είναι πάρα πολλές και οι διαφορικές εξισώσεις στις οποίες καταλήγουν είναι διαφόρων τύπων.
Ένα παράδειγμα στην κινηματική με σχετική ταχύτητα 
Βάρκα διασχίζει ποτάμι από την μια όχθη στην άλλη. Ο άξονας χχ΄ είναι κάθετα στο ρέμα και ο ψψ΄με την φορά του ρέματος. Το ποτάμι έχει σταθερή ροή νερού με ταχύτητα υπ με φορά την αρνητική κατεύθυνση του άξονα ψ. Η σχετική προς το ρέμα ταχύτητα της βάρκας είναι υβ και το διάνυσμά της κατευθύνεται πάντα προς την αρχή των αξόνων. Το μέτρο της είναι σταθερό |υβ| = υβ σταθερό. Την αναλύουμε σεταχύτητα στον άξονα των χ που είναι
υβχ = -vβ συνθ =dx/dt. και υβψ =-vβημθ =dy/dt
Η ταχύτητα της βάρκας στον άξονα των ψ είναι υβψ = -vπ-vβημθ
Ερευνώντας για τις αρχικές συνθήκες θεωρούμε ότι σε κάποια χρονική στιγμή το σύστημα δέχτηκε ώθηση ίση με την μεταβολή της ορμής Ω ή J=ΔJ
Ένα παράδειγμα της εφαρμογής της Bernoulli είναι η κίνηση σε κεκλιμένο επίπεδο.
Εδώ σαν ρευστό μπορεί να θεωρειθεί ο αέρας που προβάλει αντίσταση στην κίνηση. Η δύναμη F=ma μπορεί να αντικατασταθεί ως εξής: F=m d2 s/dt = Bx -T -A όπου Τ είναι η τριβή και Α η αντίσταση του αέρα
Την Α θεωρούμε ανάλογη του τετραγώνου της ταχύτητας Α=k (ds/dt)2 και η Τ =μmgσυνθ
m d2 s/dt2 = mgημθ - μmgσυνθ -k (ds/dt)2
που απλουστεύεται στη ΔΕ
d2 s/dt2 = gημθ - μgσυνθ -k/m (ds/dt)2
και εφόσον g, m, θ, είναι σταθερά γίνεται d2 s/dt2 = λ2 -h2 (ds/dt)2
όπου k/m=h2 και λ2=ghmθ -μgσυνθ
 Οι δυνάμεις στον ταλαντωτη είναι η τάση Τ = -kx (Η Δύναμη που ασκείται στο ελατήριο για να επιμηκυνθει κατά x είναι kx)
Οι δυνάμεις στον ταλαντωτη είναι η τάση Τ = -kx (Η Δύναμη που ασκείται στο ελατήριο για να επιμηκυνθει κατά x είναι kx) 

![]() ,
, ![]() , και
, και ![]() .
. 
 Συνηθίζονται για κινήσεις που υπόκεινται σε δεσμούς ή περιγραφή συστημάτων που αποτελούνται από Ν σώματα και μελετήθηκαν από Γάλλο μαθηματικό Joseph-Louis Lagrange (1736-1813).
Συνηθίζονται για κινήσεις που υπόκεινται σε δεσμούς ή περιγραφή συστημάτων που αποτελούνται από Ν σώματα και μελετήθηκαν από Γάλλο μαθηματικό Joseph-Louis Lagrange (1736-1813). ![]()



